Thorsten Schlaak & Manfred Schwarz
Von der (Un-)Möglichkeit, zu steuern, und wie man trotzdem ans Ziel kommt
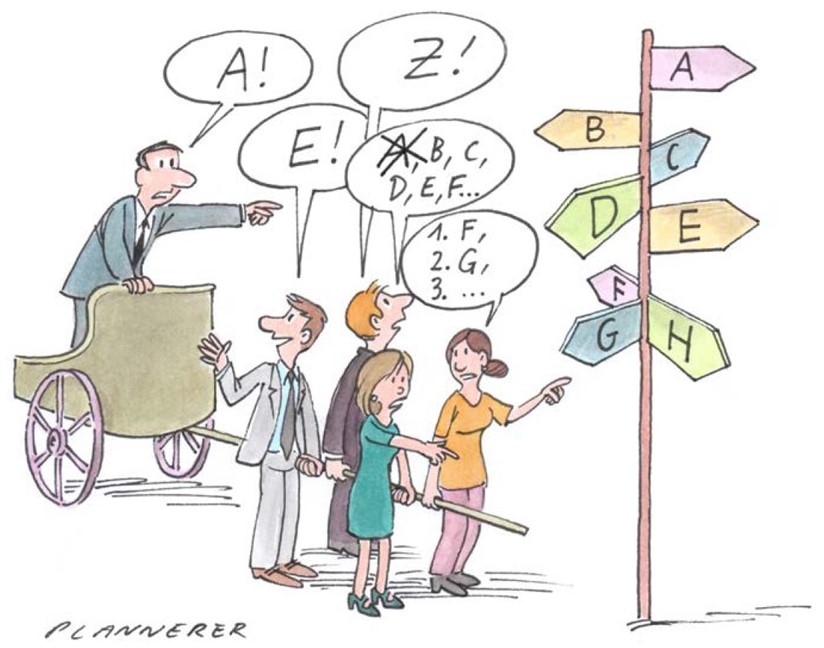
In unsteten Zeiten wie diesen − VUCA und Corona seien hier beispielhaft genannt − glaubt wohl niemand mehr daran, dass jedes System, berechenbar, beherrschbar und steuerbar ist. Die Erfahrung lehrt: Systeme zeigen bisweilen »ungehöriges« Verhalten. Doch wie »unberechenbar« kann ein System eigentlich sein?
Ein Bügeleisen sollte, sobald es unter Strom steht, heiß werden. Und sobald der Netzstecker gezogen wird, wieder erkalten. Entweder ein oder aus. Maschinen funktionieren, sind bestimmbar, berechenbar. Einzelteile können ausgetauscht werden, die Maschine kann ein- und ausgeschaltet, zerlegt und wieder zusammengebaut werden: Eine einfache Maschine wie ein Bügeleisen lernt nicht und entwickelt sich nicht. Sie ist immer ein Input-Output-Modell.
Und wie sieht es im Zusammenspiel von Menschen aus? Im alltäglichen Zusammenleben ist oft ein gewisses Maß an Trivialität hilfreich, etwa um sich schnell orientieren zu können, z. B. an einer Fußgängerampel.
Im Gegensatz dazu existieren soziale Systeme immer in wechselseitiger Beeinflussung mit ihren Umwelten. Im Umgang damit müssen wir immer mit Komplexität rechnen. Und es existiert kein fixes Modell oder keine Formel, nach denen ein bestimmtes Ergebnis berechenbar wäre. Die Zustände eines Systems sind immer wechselwirkend und dynamisch.
Zum Nachdenken und Nachrechnen
Was hat Steuern mit trivial oder nicht-trivial zu tun?
Heinz von Foerster, einer der Wegbereiter des Konstruktivismus, ist u. a. der »Erfinder« der Kybernetik zweiter Ordnung. Ihm verdanken wir auch die Unterscheidung zwischen trivialen und nicht-trivialen Maschinen:
Triviale Maschinen arbeiten mit einer einfachen Input-Output-Relation: Sie reagieren auf den gleichen Input immer mit dem gleichen Output. Wenn die Funktion (f) z. B. x + 3 lautet, wirft diese Maschine für x = 2 das Ergebnis y = 5, für x = 5 entsprechend y = 8 aus, usw. Alles vorhersagbar und damit trivial.

Abbildung: Triviale Maschine (nach von Foerster, 1993, S. 357 ff.)
Aufgabe:
Stellen Sie sich nun vor, Sie haben eine Box mit vier verschiedenen Schaltern und Lampen (jeweils blau, grün, gelb und rot). Diese tut immer dasselbe und ist in ihrem Verhalten absolut berechenbar. Wenn Sie einen Schalter drücken, leuchtet die zugehörige Lampe auf. Wie viele Varianten dieser Maschine gibt es?
Das Gegenstück sind nicht-triviale Maschinen: Sie funktionieren ganz anders. Zum Beispiel verändern sie je nach Input und in Abhängigkeit von ihrem inneren Zustand sowohl ihren inneren Zustand als auch ihre endgültige Funktion.

Abbildung: Nicht-triviale Maschine (nach von Foerster, 1993, S. 357 ff.)
Warum diese Maschinen alles andere als trivial sind, soll eine kleine Überlegung zeigen: Nehmen wir an, Ihre nicht-triviale Maschine hat für den Input wiederum vier mögliche Werte (Rot, Blau, Grün, Gelb), als Output-Möglichkeit, aber nur zwei Zeichen (+ und −). Y sei die Wirkungsfunktion, z‚ die Zustandsfunktion.

Das heißt: Befindet sich die Maschine z. B. im Zustand Z = B und Sie geben Rot ein, so wirft sie ein »−« aus, wechselt aber sogleich in den Zustand Z = A. Geben Sie nun wieder ein Rot ein, gibt sie »+« aus.
2. Aufgabe: Wie viele nicht-triviale Varianten dieses Typs, also mit vier Input-Möglichkeiten, zwei Outputs sowie zwei inneren Zuständen gibt es?
Hintergrund
Vielleicht haben Sie das Ergebnis der zweiten Aufgabe schon ermittelt. Wenn nicht: So viel sei verraten, es ist höher als gedacht. Natürlich folgt auch die nicht-triviale Maschine festen Regeln. Wer diese Regeln aber nicht kennt, hat nur geringe Chancen, deren Funktionsweise zu ergründen.
Psychische und soziale Systeme sind immer nicht-trivial. Aufgrund ihrer Fähigkeit, innere Bilder und Landkarten von der Außenwelt zu entwickeln, entsteht eine hohe Eigenkomplexität. Damit können sie die aus ihren Umwelten ausgewählten Daten mit systemeigenen Daten anreichern und verknüpfen. So muss das System, um handlungsfähig zu bleiben, die eigene systemspezifische Komplexität in einem Selektionsprozess wieder reduzieren und in machbare Handlungsoptionen umwandeln.
Für die Praxis
Was heißt das nun für das Arbeiten mit Systemen wie einem Team, einer Gruppe, einem Unternehmen, einer Familie oder z. B. einem Freundeskreis? Die Umwelt liefert einen Input und wirkt somit auf das System ein. Diese »Umwelt« könnten Sie sein. Etwa, wenn Sie z. B. bewirken wollen, dass einer Ihrer Mitarbeiter in Zukunft pünktlich zu Besprechungen erscheint. Konkret: Sie sagen diesem Mitarbeiter einmal, was Sie wollen. Was passiert wohl? Folgt die erwartete Wirkung und am Ende ein neues Verhalten? Eins zu eins wie beim Uhrwerk?
Bei einem trivialen, mechanistischen Bild funktioniert eine klare BefehlsGehor sam-Struktur. Die Erfahrung lehrt uns etwas anderes: Mit einiger Wahrscheinlichkeit zeigt der angesprochene Mitarbeiter nicht die erwartete Wirkung. Er spielt nicht mit – führt also weiterhin mehr oder weniger gute Gründe dafür an, dass er mal wieder zu spät kommt.
Das System organisiert sich selbst
Der systemische Blick hilft weiter. Die Grundidee dahinter: Das System organisiert sich selbst.

Abbildung: Mögliche Reaktionen des Systems auf einen Input der Umwelt
Hier regt die Umwelt das System an, sie gibt einen Impuls. Und was macht das System? Es kann ganz unterschiedlich reagieren:
– den Impuls abwehren oder sich gar auflösen (etwa wenn die Anforderung aus der Umwelt zu groß ist),
– gar nicht reagieren,
– sich neu organisieren.
Am Ende gibt es also nur »mögliche« Wirkungen. Mehr kann man – aus der systemischen Sichtweise – nicht sagen. Zwar geht Gewissheit verloren, da es kein einfaches Ursache-Wirkungs-Verhältnis gibt, aber wir gewinnen Praxisnähe. Das systemische Bild eines Impulses geht über das mechanistische Verständnis hinaus. Dementsprechend sind die Möglichkeiten, zu »steuern«, eingeschränkt, denn Impulse können nur als Interventionen und Anregungen für ein System verstanden werden. Konkret bedeutet das:
Ist die Anregung
- zu groß, erfolgt wahrscheinlich Abwehr;
- zu klein, wird sie eventuell gar nicht erst erkannt;
- passgenau, ist Neuorganisation möglich.
Es lohnt sich also, jederzeit achtsam zu sein und das System als Ganzes, eben systemisch im Blick zu haben.
Die Lösungen der beiden Aufgaben
- Die triviale Maschine mit ihren vier Schaltern und Lampen gibt es in 4! (Fakultät) Varianten, also in 24 Varianten.
- Die Lösung der zweiten Aufgabe liegt bei 6 x 10 hoch 76.
Das hört sich nicht nur gigantisch an, sondern ist es auch, zumal wenn man diese Zahl mit der Anzahl aller Protonen und Elektronen im Universum (nach Eddington und Dirac) vergleicht: Sie liegt bei 1,2 x 10 hoch 80.
(Siehe für die Lösung den Link: Schröder und die Visualisierung: YouTube: Blackbox.)
